摄影测量标定参数介绍

  高速摄像机标定是摄影测量与真实三维世界测量的联系桥梁，通过标定，可将高速摄像机拍摄到的二维图像像素转换为物理世界的三维测量单位。因此，标定是摄影测量及三维场景重构的关键。

  高速摄像机标定包括高速摄像机几何模型和透镜的畸变模型，这两个模型定义了高速摄像机的内参数（intrinsic parameter）。在描述真实三维空间世界坐标时，需要明确真实三维空间坐标与高速摄像机坐标的对应关系，这个对应关系定义了相机的外参数。

  下面让我们来介绍内参数和外参数的细节：

高速摄像机几何模型：

  高速摄像机几何模型需要考虑焦距f，即，投影中心到图像平面的距离。由于单个像素在低成本的成像仪上是矩形而不是正方形，因此需要单独考虑x轴和y轴上的焦距f_x, f_y。

  当芯片中心在光轴上时， 针孔高速摄像机模型本可以用一个简单的相似三角形比例式子表示：

  成像仪上的图像坐标x=f_x *（物长/物距）

  但是，由于芯片中心通常不在光轴上，所以需要引入芯片中心相对于光轴的偏离值c_x,c_y。

  综上，相机几何模型可表示为：

x_screen=f_x(x/z)+c_x

y_screen=f_y(Y/Z)+c_y

透镜畸变模型：

  第一种畸变是径向畸变。高速摄像机的透镜总在成像仪的边缘产生显著的畸变（类似于桶形畸变），即，光线在远离透镜中心的地方比靠近中心的地方更加弯曲，该现象可以用如下来衡量(引入畸变参数k₁,k₂,k₃…)：

x_corrected=x(1+k₁r²+k₂r⁴+k₃r⁶)

y_corrected=y(1+k₁r²+k₂r⁴+k₃r⁶)

  第二种畸变是切向畸变。这种畸变是由于透镜制造商的缺陷使透镜本身与图像平面不平行产生的，公式如下(引入畸变参数p₁,p₂)：

                                    x_corrected=x+[2 p₁ y+ p₂ (r²+2x²)]

                                    y_corrected=y+[p₁(r²+2y²)+2p₂x]

外参数：

  如果仅采用单目测量，仅需要对高速摄像机进行内参标定即可。如果采用双目高速摄像机或者在一些需要将真实三维空间与高速摄像机坐标系建立关系的场合时，才需要进行外参数标定。

  外参数包括相对于x轴、y轴、z轴的旋转角度和平移向量，通过获取这些参数，可以将世界坐标转换到相机坐标：

相机坐标系坐标=R（世界坐标-T）

  绕x轴、y轴、z轴的旋转矩阵如下：

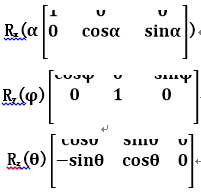
应用案例分析：

  深圳市仰望科技有限公司开发的铁轨轨廓测量系统，能够通过3D激光线检测出铁轨断面、铁轨垂直磨损、轨道廓形、运动半径、轨头高度、侧边磨损等各种轨形参数。

  首先，需要先对系统进行内参数标定，获取高速摄像机几何模型及镜头畸变模型。其次，该系统激光线相对高速摄像机静止，因此可以采用外参标定的方法获取激光线所在的世界坐标相对于高速摄像机坐标的转换关系。这样，通过相机芯片上的激光线所占像素格式即可获取铁轨的实际尺寸，测量精度高达0.1mm。